√1000以上 立方体 面積分 976598-面積分 例題 立方体
楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ
体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう！ここで体積を として今までの結果をまとめると以下のような式になります。 まずは について積分を行い線の長さを計算します。 次に線の長さ× の積分を行い面積を計算します。 最後に面積× の積分を行い体積を計算する流れになります。 このように考えると積分は点⇒線⇒面⇒立体ということがイメージできるのではないでしょうか？ 次の記事では実際に例題
面積分 例題 立方体
面積分 例題 立方体-立方体の表面積を求める公式 表面積=辺の長さ×辺の長さ×6 辺の長さ4cmの立方体 → 4cm×4cm×6 → 96cm 2 単位が違う場合の計算方法 辺の長さと面積で単位が違う場合は、面積の単位に辺の長さをあわせてから計算をおこないます 辺の長さ0cm、面積?m 2 → 2m×2m×6 → 24m 2 面積から辺の 面積分、体積分、ふつうの積分の理解は写真のような感じでいいですか？ 面積分→面をあつめて面をつくる 体積分→立方体をあつめて立方体をつくる ふつうの積分→線をあつめて面をつくる
講師 幹 浩文 A314 微分 ベクトル解析 14 講師 幹 浩文 A314 A１03 10 50 12 金 Ppt Download
Cm³の立方体の何こ分か計算で求めてみましょう。 1 cm³ の立方体が何こあるのかを求めるには？？ ・面積のときは計算で求められたなぁ。 ・その計算は、かけ算の式で表すことができた。 ・たてにならぶ数 と 横にならぶ数をかけて求めた。 年生で学習した 使えば、 求められそうだね0≦x≦1, 0≦y≦1, 0≦z≦1} の表面です。 いろいろ考えたのですが、どうも計算が煩雑になりすぎてうまくいきません。 曲座標変換も考えたのですが、立方体上の積分ではうまくいきませんでした。ベクトル解析における面積分（めんせきぶん、surface integral）は、曲面上でとった定積分であり、二重積分として捉えることもできる。線積分は一次元の類似物にあたる。曲面が与えられたとき、その上のスカラー場やベクトル場を積分することができる。 面積分は物理学、特に電磁気学の古典論に応用がある。 面積分の定義は、曲面を小さな面素へ分解する
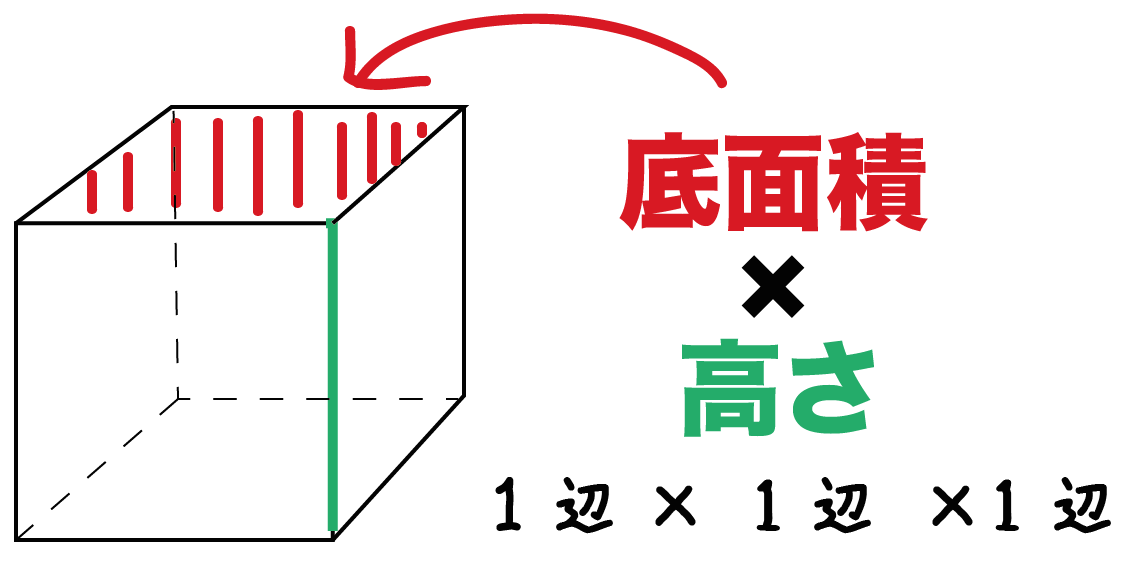
面積分 dS z = f (x, y) z x y 領域 上で 関数 の積分を考える．f を微小領域に分解し，そのそれ ぞれの微小領域を底面とし高さ を持つ柱体を考える． f この柱体の(符号も込めた)体積はf dS 微小領域の面積をdSと書けば 面積要素 f dS これらを領域 で全部足し合わせたものを，関数 の 領域 上での面積分といい と表す． f もちろん は領域 の面積である． いろいろな図形上の面積分 1 0 1y 0 f (x, y)dxdy1辺が1cmの立方体の体積が1㎤ です。 今から公式が成り立つ理由を説明する上で重要となりますので、必ず理解をしてください。 立体図形② 直方体の面積「たて×横×高さ」立方体の面積「1辺×1辺×1辺」が成り立つ理由立方体の体積は （1辺）×（1辺）×（1辺） で求めることができ 立方体の表面積Sは「一辺の長さの2乗に6を掛けた値」です。公式はS=6a 2 です。直方体の表面積Sは「S=2ab2ac2bc」で計算できます。立方体、表面積の意味など下記も勉強しましょう。 立方体の公式は？1分でわかる意味、体積の公式と例題の求め方、表面積の 同じ体積の球と立方体では
面積分 例題 立方体のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
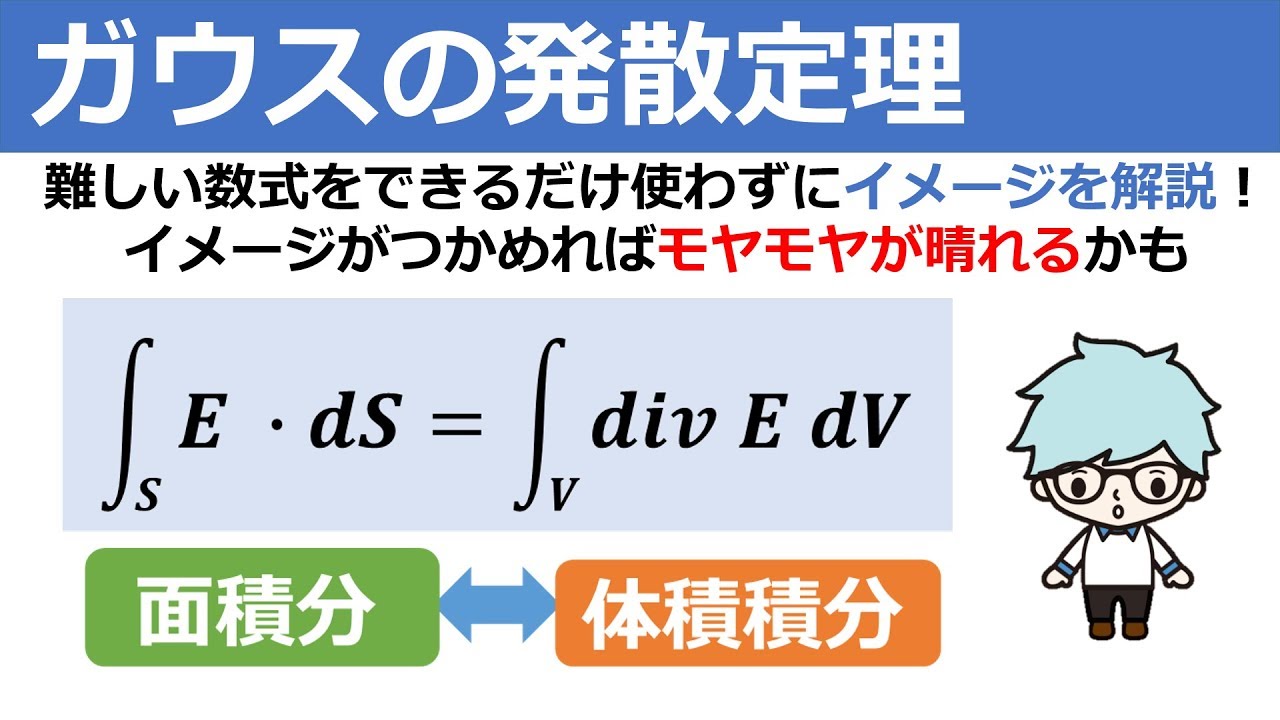 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | 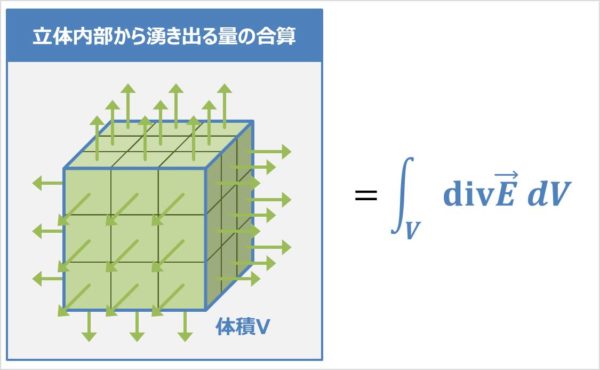 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
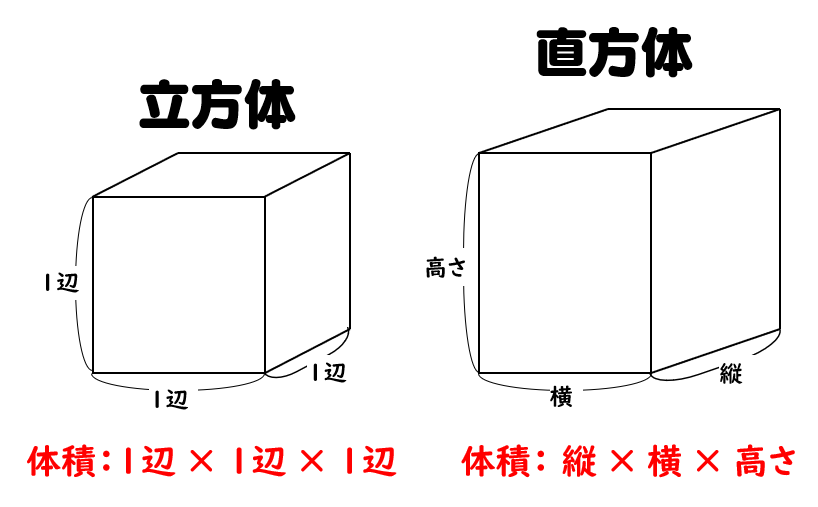 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | 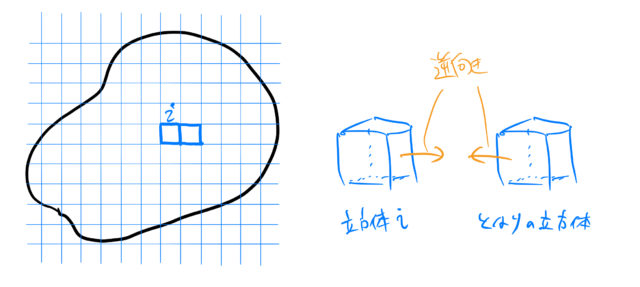 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
「面積分 例題 立方体」の画像ギャラリー、詳細は各画像をクリックしてください。
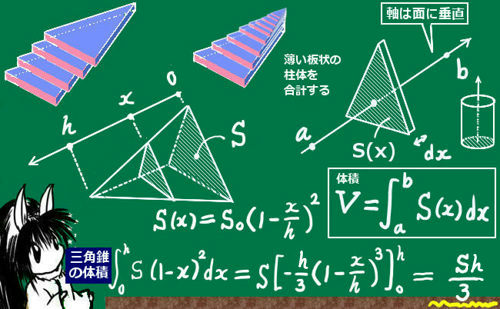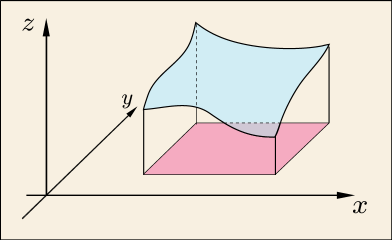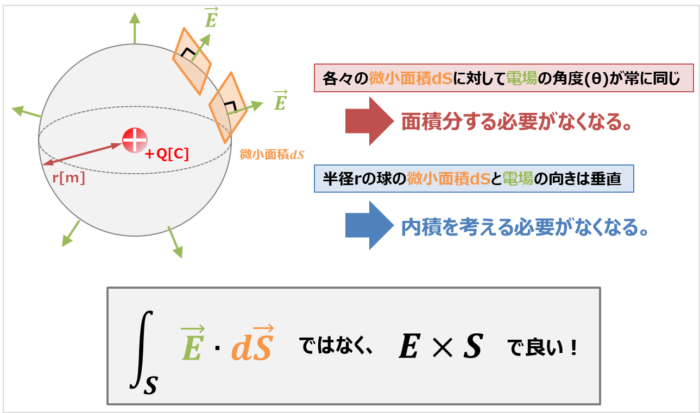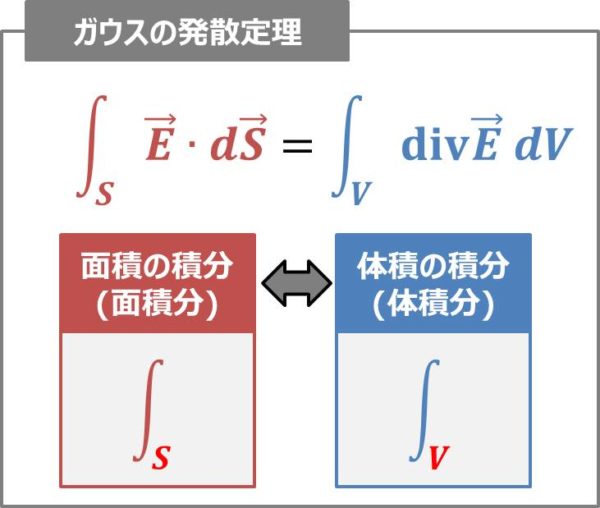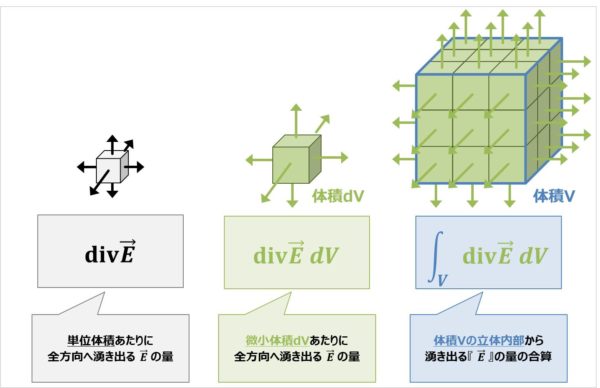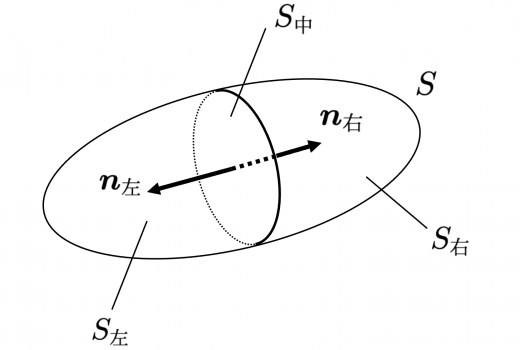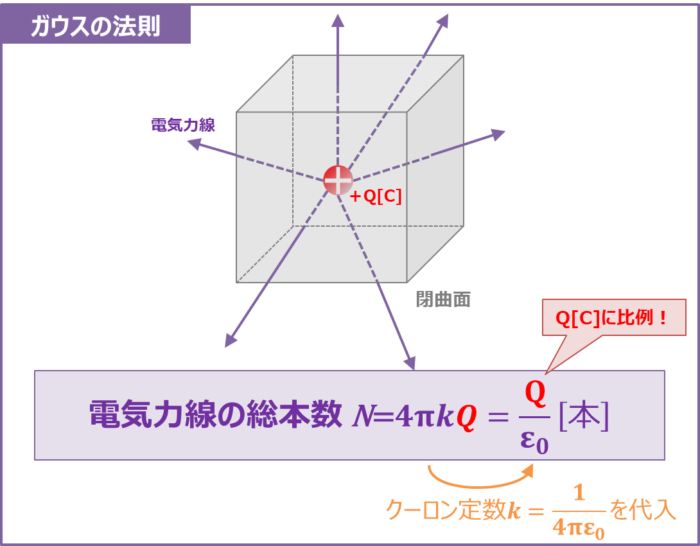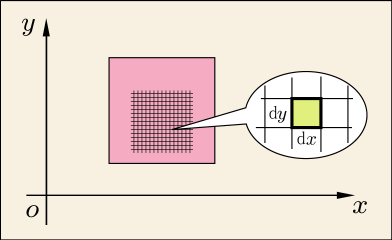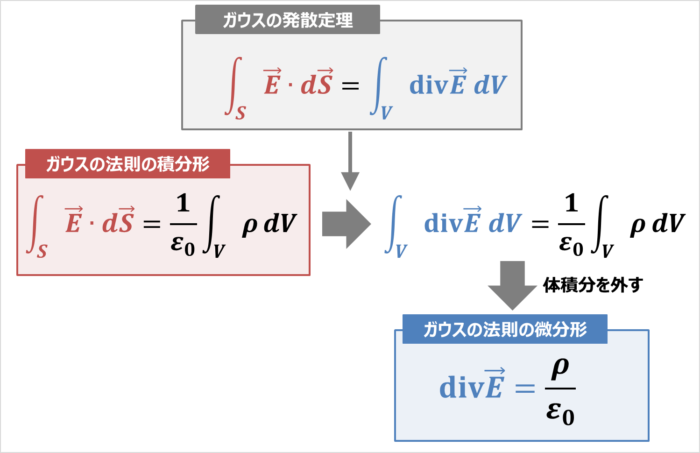 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |  この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |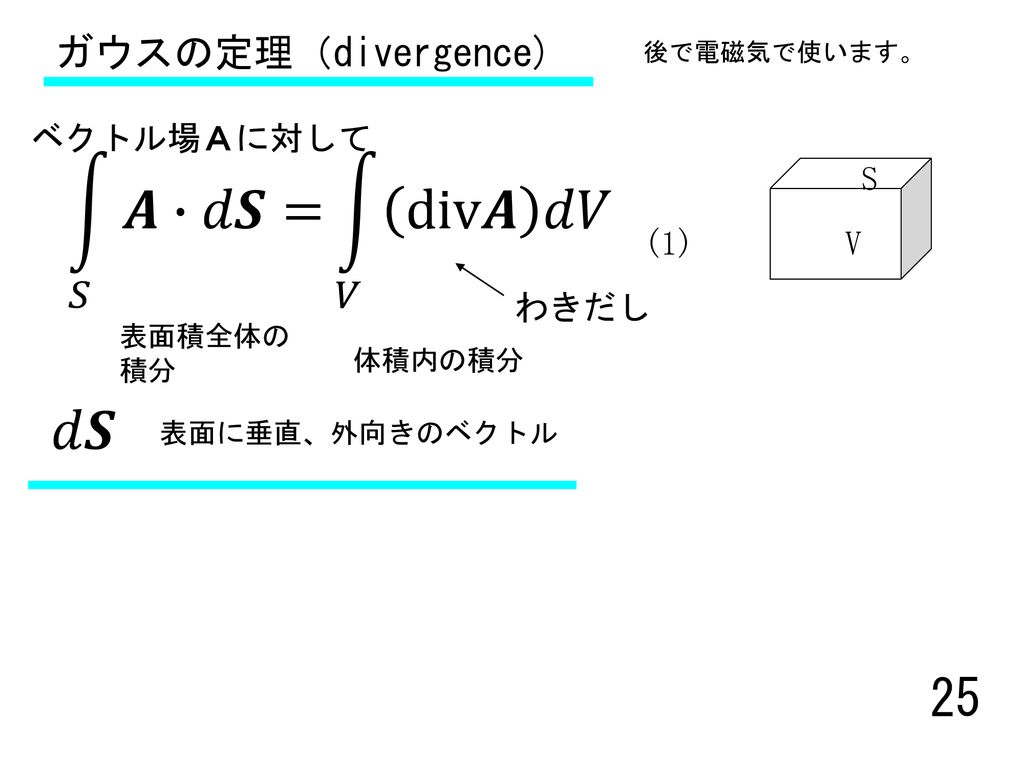
 この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote | この問題がよく分かりません 1 1 1の立方体を入れればこの直方体の体積分 Clearnote |
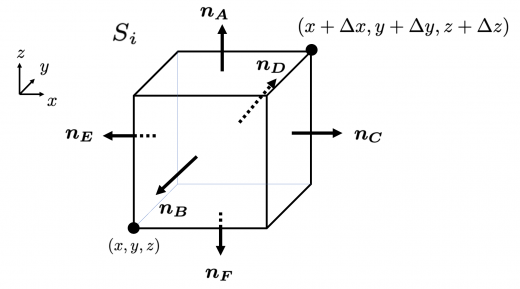
面積分とは ある曲面 S 上で定義されるスカラー場 F に対し、 ∫ S F d S を F の S 上での 面積分 といいます。 ここで、 dS は S 上の微小面積素です。 曲面 S が閉曲面の場合、 ∮ S F d S と書きます。 ベクトル場の面積分 ベクトル場 F を考えます。 曲面 S の単位法線ベクトルを n とすると F・n はスカラー場となります。 これを F とおいて面積分すると、 ∫ S F d S = ∫ S F ・ nd S となります。 ここ 立方体は同じ形状の6つの面で構成されているため、問題の条件で表面積の合計（S）が与えられた場合、面の対角（l）を計算するには、前のステップの式を少し変更すれば十分です。 その中で全面積の6分の1の1つの面の面積を置き換えます。 l =√（2 * S / 6
Incoming Term: 立方体 面積分, 面積分 例題 立方体,
コメント
コメントを投稿